1.1. HCFとS-N曲線（ウェーラー線図）の基礎

1.1. HCFとS-N曲線（ウェーラー線図）の基礎
（Basics of HCF and S-N curve (Wöhler diagram)）

 

スポンサーリンク

アフィリエイト広告を利用しています。

 

 

1.1.1. 高サイクル疲労（HCF : High Cycle Fatigue）とS-N曲線（ウェーラー線図）の定義と基礎

高サイクル疲労（HCF）は、一般的に低応力振幅かつ高サイクル数の領域で発生する疲労条件を指し、通常は$10^6$または$10^7$サイクル以上で評価されます。HCFは、通常、高周波数、低振幅、そして公称弾性的な繰り返し挙動を伴う疲労状態であるとされています。応力-ひずみ曲線上で純粋な弾性挙動が高サイクル疲労に、塑性挙動が低サイクル疲労（LCF : Low Cycle Fatigue）に関連付けられることがありますが、この定義は厳密ではありません。LCFが通常は、材料の耐力以上の負荷をかけるひずみ制御条件（ε-N曲線）下で実施されるのに対し、HCFは一般的に、材料の耐力以下の負荷をかける荷重制御条件（S-N曲線）下で実施されます。
HCFの挙動を特性化するための最も基本的なツールは、S-N曲線（ストレス-ライフ曲線、またはウェーラー線図）です。S-N曲線は、一定の応力比（\( R=\sigma_{ min }/\sigma_{ max } \)）の下で、最大応力（S）を破断サイクル数（N）の関数として片対数グラフにプロットしたものであり、材料の疲労特性を示す基本的な図として機能します。S-N曲線は、しばしばウェーラー線図（Wöhler diagram）とも呼ばれますが、これは1800年代後半に最初の大規模な疲労試験を実施し「疲労の父」と呼ばれるアウグスト・ウェーラー（August Wöhler）にちなんでいます。
HCFは、ウェーラーが初期の研究を行った鉄道の車軸や橋梁の事故に関連する繰り返し荷重の問題として、1800年代にその重要性が認識され始めました。S-N曲線は、応力比Rが一定の試験データに基づいて描かれ、Rの値が異なると別の曲線が必要になります。設計上、HCFはS-N曲線において、サイクル数が非常に大きく（通常\( 10^7 \)サイクル以上）、曲線が水平に近づく右端の領域に対応します。この領域では、サイクル数が大きすぎるために、高い信頼性をもって材料特性を特徴づけるための統計的に有意なデータを十分に取得することが困難になるという課題があります。

 

1.1.2. 疲労限度応力（FLS）と耐久限度（エンデュランス・リミット）の概念

高サイクル疲労（HCF）設計における中心概念は、疲労限度応力（Fatigue Limit Stress: FLS）または耐久限度（Endurance Limit）です。これらの応力レベルは、材料が破壊に至らないとされる（無限寿命を保証する）水準を指します。
理想的なS-N曲線においては、あるサイクル数（例えば\( 10^7 \)サイクル）を超えると曲線が水平な漸近線となり、この応力レベルが耐久限度（Endurance Limit）と見なされます。この水平な漸近線が存在する材料は、その応力レベル以下であれば「無限寿命」が保証されると仮定されます。
しかしながら、現実の工学的な取り扱いにおいては、真の無限寿命（Endurance Limit）を実験的に証明することは不可能です。無限寿命を保証する実験を実施することはできないので、この耐久限度は、工学的な近似として取り扱われます。
実務上は、疲労限度応力（FLS : Fatigue Limit Stress）または疲労限度（Fatigue Limit）という用語が、特定の長いサイクル数（通常\( 10^7 \)サイクル以上）に対応する応力レベルを指すものとして、耐久限度の代わりに用いられることが一般的です。疲労限度応力（FLS）は、材料が生き残る応力、すなわちランアウト応力（run-out stress）とも呼ばれますが、特定サイクル数に対応する疲労限度応力（FLS）と呼ぶ方が、より正確です。
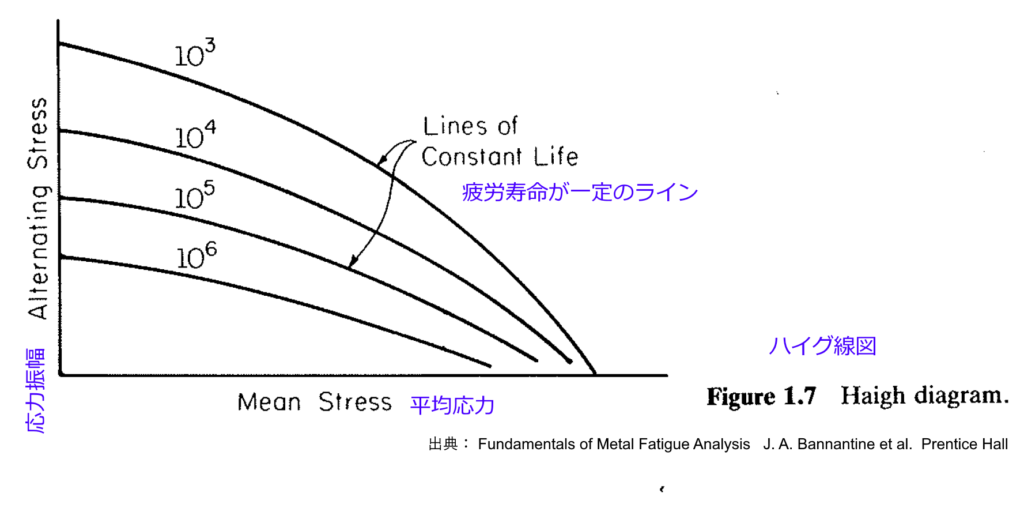
疲労限度応力（FLS）の値を求める方法としては、S-N曲線上で目的のサイクル数（例：\( 10^7 \)サイクル）におけるデータ点を用いるか、またはデータをそのサイクル数まで外挿して求めることが一般的です。この疲労限度応力（FLS）は、応力比Rを固定したS-N曲線から得られた後、通常、平均応力（\( \sigma_{ m } \)）と交番応力（\( \sigma_{ a } \)）をプロットしたハイグ線図（Haigh diagram）上に整理され、設計の基準線として用いられます。このハイグ図は、HCFにおける疲労限度の値を重視してデータを表示する図であり、定寿命線図（Constant Life Diagram）の一種です。

図　Haigh線図　　出典： Fundamentals of Metal Fatigue Analysis J. A. Bannantine et al. Prentice Hall

 

1.1.3. ギガサイクル疲労（GCF）現象とS-N曲線の下降傾向

本コンテンツで、ギガサイクル疲労（gigacycle fatigue）というタームを使用しますが、一般的には超高サイクル疲労（VHCF：very high cycle fatigue）、超長寿命疲労（Ultra-long life fatigue）として知られています。サイクル数が\( 10^7 \)回を超える寿命域で疲労破壊を生じ、疲労強度がこの寿命域でさらに低下する疲労を言います。
ギガサイクル疲労は、\( 10^9 \)回に相当する繰返し数の疲労を意味します。実際の製品を例にすると、約10年の使用で、自動車のエンジンや駆動用部品では\( 10^8 \)回相当以上の繰返し数、新幹線の車軸では\( 10^9 \)回相当の繰返し数が負荷されることになります。
従来の高サイクル疲労（HCF）設計では、\( 10^7 \)サイクルを疲労限度と見なしています。
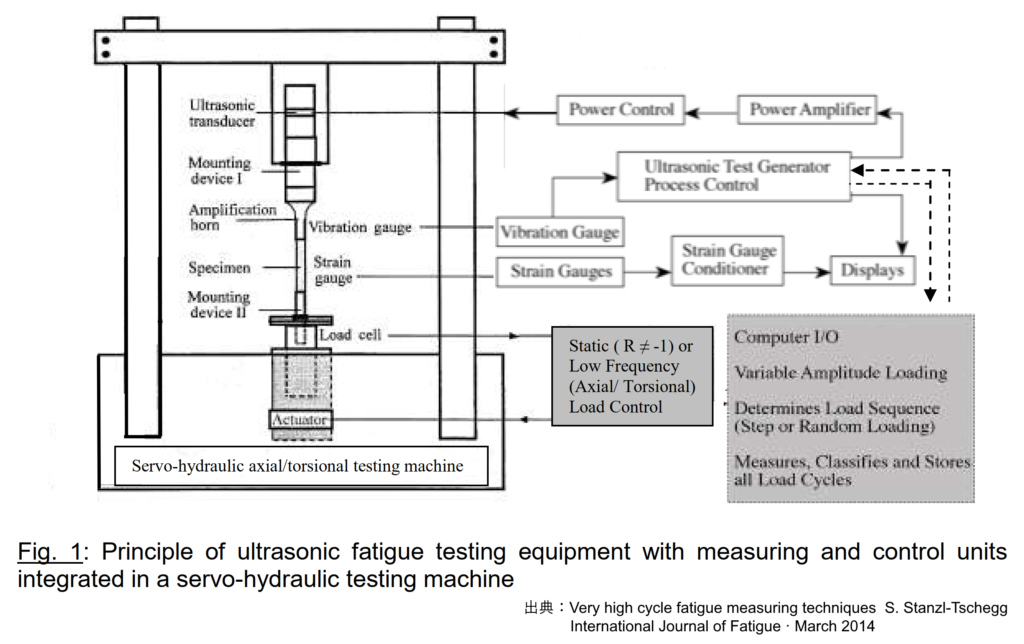
近年、ギガサイクル疲労（GCF：Gigacycle Fatigue）と呼ばれる\( 10^9 \)サイクル以上の超長寿命域での疲労挙動が注目されています。ギガサイクル疲労（GCF）領域のデータを効率的に収集するためには、超音波試験機（20 kHzなど）を用いる加速試験技術が不可欠です。
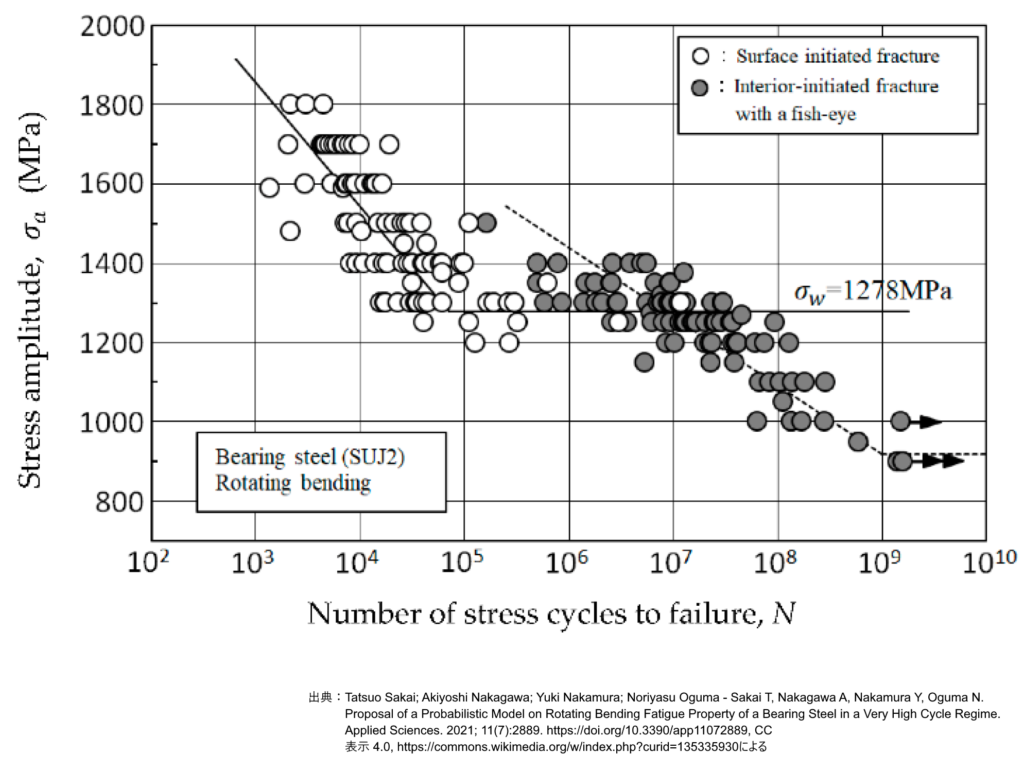
ギガサイクル疲労（GCF）領域の研究により、一部の材料（高強度鋼やチタン合金など）において、従来の\( 10^7 \)サイクル付近で見られる水平な疲労限度を超えて、S-N曲線が再びわずかに下降し続ける現象が確認されています。この挙動は、S-N曲線が二つの勾配を持つ二重S-N曲線（Duplex S-N curve）、あるいは二重S-N線図、二重S-N特性とばれます。図は、高強度鋼（SUJ2）の二重S-N曲線の例を示します。

図　二重S-N曲線の例；SUJ2　　出典： https://commons.wikimedia.org/w/index.php?

S-N曲線が超長寿命域で下降する現象は、多くの場合ば破壊起点の変化（Change in Failure Mechanism）に強く関連しています。従来から用いられている\( 10^7 \)回繰返し数までの高サイクル疲労（HCF）域では、材料表面の欠陥や応力集中部に起因する表面起点（Surface initiation）破壊が支配的ですが、超長寿命域のギガサイクル疲労（GCF）域では、材料内部の微小な欠陥や介在物からの内部起点（Subsurface initiation）破壊が支配的になることが示されています。
内部起点破壊が発生する場合、き裂発生箇所が空気などの環境から隔離されているため、表面き裂の進展に影響を与える環境要因が排除され、結果的に疲労寿命が延びる一因となります。この内部起点破壊の破面（フラクトグラフィ）には、起点となった内部欠陥を中心とした同心円状のフィッシュアイ（fish-eye）模様が特徴的に観察されます。フィッシュアイの領域は、介在物を起点に始まった疲労き裂が進展していった跡と考えられています。フィッシュアイの⼤きさは、0.5 mm から 1 mm 程度であることが多いです。
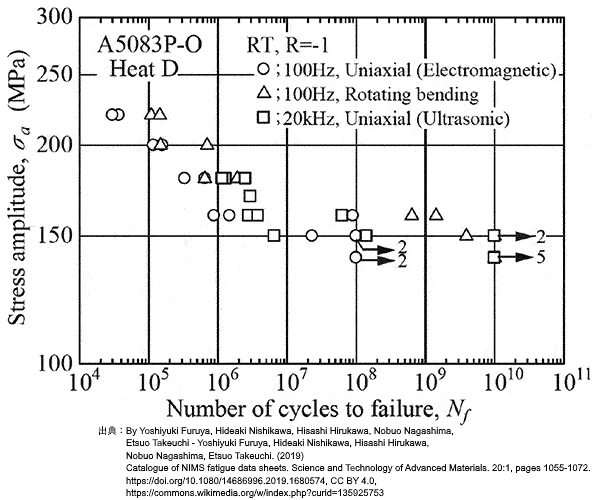
ギガサイクル疲労（GCF）の研究は、疲労限度の概念を工学的近似として扱う傾向を強くなってきています。材料によっては\( 10^9 \)サイクルを超えても疲労限度が確認されない場合がある一方で、ある種のアルミニウム合金では、\( 10^{ 10 } \)サイクルを超えても破壊しない疲労限度を示す例も報告されています。

図　アルミニウム合金の超高サイクル疲労S-N曲線　出典：https://commons.wikimedia.org/w/index.php?

 

1.1.4. 高サイクル疲労（HCF）データにおける統計的ばらつきの課題

高サイクル疲労（HCF）設計における大きな課題の一つは、S-N曲線が平坦に近づく長寿命領域では、特定の応力レベルでの寿命のばらつき（散乱/Scatter）が非常に大きくなることです。この散乱の増加は、S-N曲線が水平に近くなることによって、わずかな疲労強度の違いが非常に大きな寿命の差として現れるためであり、これはHCF寿命が対数軸上でプロットされることからも顕著になります。
このため、HCF設計に利用するためには、平均的なデータ（中央値）だけでなく、統計的有意性を持ったデータ、例えば90%または99%信頼区間の下限値、あるいは正規分布を仮定した際の\( \text{-}2\sigma \)や\( \text{-}3\sigma \)の最小値を確立する必要があります。実務上、信頼性の確保のためには、材料のばらつきを考慮に入れた許容応力（アロワブル）を設定することが不可欠です。
ばらつきの統計的評価の難しさは、適用された荷重（振動応力など）のばらつき、および材料自体の能力のばらつきの両方の分布関数の末端（テールエンド）についてほとんど情報がないことにも起因します。特に、設計上最も重要な分布関数の下限側（低確率側の限界）を推定する際には、仮定する分布関数（正規分布、SEV分布、ワイブル分布など）の形状に結果が非常に敏感になります。

図　寿命分布を考慮したS-N曲線　　出典：High Cycle Fatigue　　Theodore Nicholas ELSEVIER 2006年

この課題に対処するため、ランダム疲労限度（RFL）モデルのような統計的アプローチが開発されています。RFLモデルでは、疲労限度が単一の定数ではなく、各試験片に固有の統計的な変数として扱われ、S-N曲線が平坦になること、およびHCF寿命における散乱が増大することを同時に説明できます。この種の統計的解析は、FLSの平均値だけでなく、設計に必須な最小疲労強度を精度良く推定するために重要となります。

 

1.1.5. FLSおよび分散を決定するための加速試験技術：階段法とステップテスト法

高サイクル疲労（HCF）の設計限度であるFLSを決定するためには、多数の試験片を長サイクルまで試験する必要があり、時間とコストの制約が大きくなります。この非効率性に対処するために、疲労限度応力（FLS）の統計的な特性（平均値と分散）を効率的に決定するための加速試験技術が採用されています。
代表的な加速試験法としては、階段法（Staircase Method）とステップテスト法（Step Test Procedure）があります。

階段法（Staircase Method）：

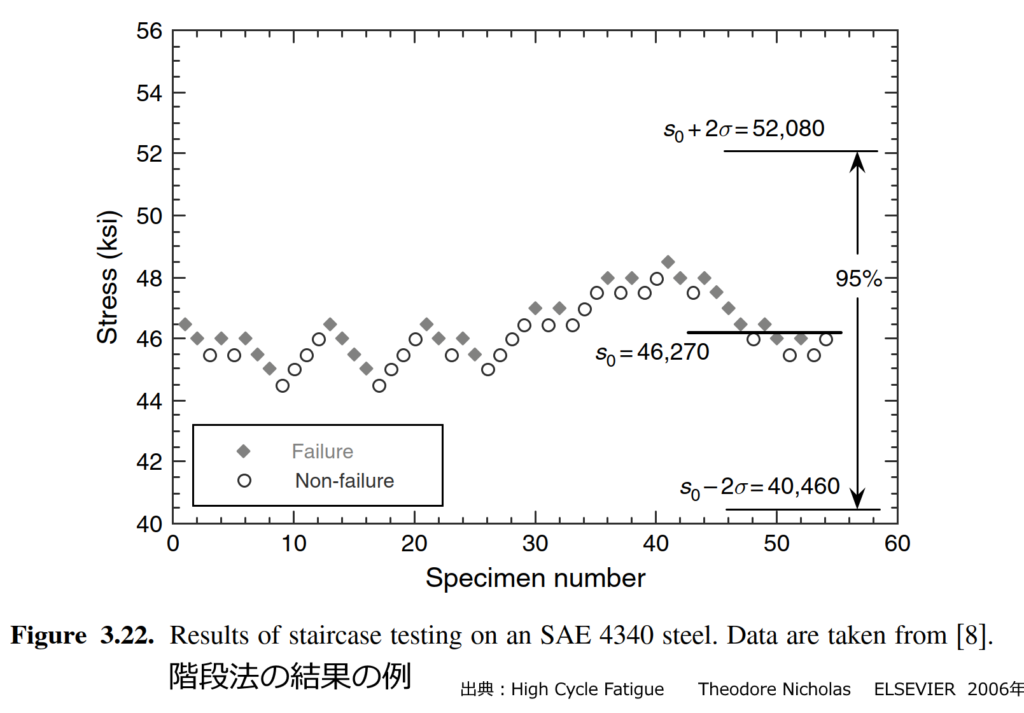
階段法（アップ・アンド・ダウン法とも呼ばれます）は、あらかじめ設定されたサイクル数（高サイクル疲労（HCF）の定義サイクル数、例：\( 10^7 \)サイクル）で試験を打ち切り、前の試験片の結果（破壊したか/生き残ったか）に応じて、次の試験の応力レベルを一定のステップサイズで上下させる手法です。この統計的手法は、特定のサイクル数における疲労限度応力（FLS）の中央値（Mean value）と標準偏差（Standard Deviation）を効率的に推定するために利用されます。階段法は、平均値の推定精度が高いという利点がありますが、試験が中央値付近に集中するため、分布の両端（設計に重要な低確率側の限界）に関する情報は限定的です。この方法の統計的解析には、Dixon and Moodの式が一般的に用いられ、FLSが正規分布に従うと仮定して平均と標準偏差が計算されます。

図　階段法により結果　　出典：High Cycle Fatigue　　Theodore Nicholas ELSEVIER 2006年

ステップテスト法（Step Test Procedure）：

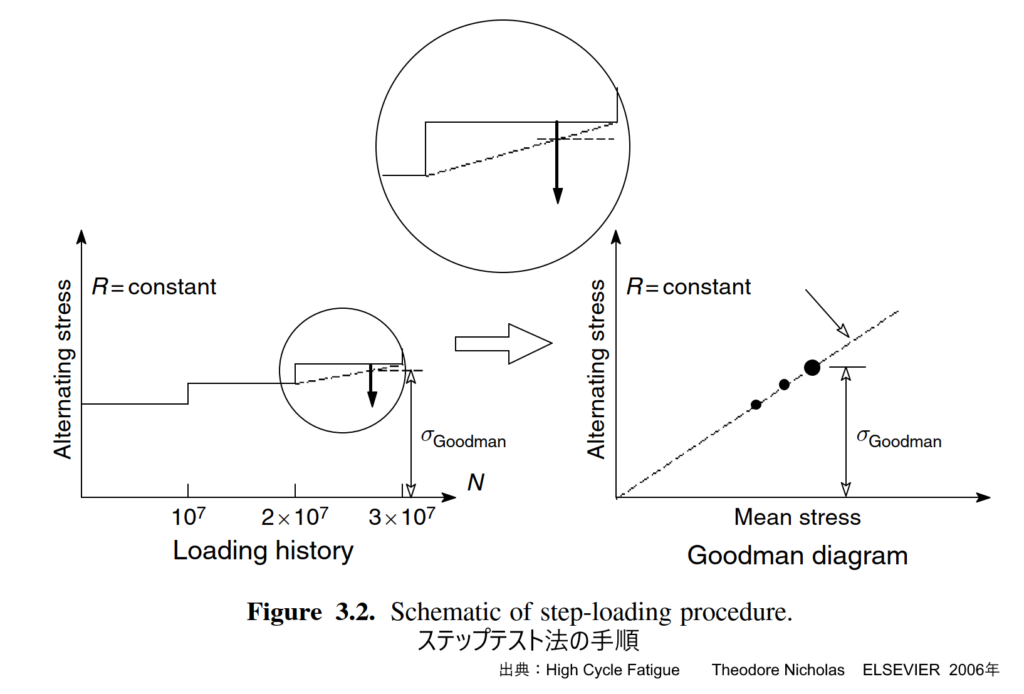
ステップテスト法は、単一の試験片に対して応力レベルを段階的に増加（または減少）させていき、最終的な破壊応力（または生き残り応力）から疲労限度応力（FLS）を推定する手法です。この方法では、各試験片から疲労限度応力（FLS）のデータ点が得られるため、限られたサンプル数でハイグ図（Haigh diagram）を作成するのに特に有用です。ステップテストは、従来の定応力S-N試験から補間して得られた疲労限度応力（FLS）と一致することが検証されており、特に高い応力比（高平均応力）領域でのデータ取得において、大幅な試験時間の短縮をもたらすことが示されています。ステップテスト法の精度は、応力履歴効果（例：前段階の荷重による影響）がないという仮定の下で疲労限度応力（FLS）を推定することに依存しますが、この仮定は一部の材料と試験条件で検証されています。

図　ステップテスト法の手順　　出典：High Cycle Fatigue　　Theodore Nicholas ELSEVIER 2006年

これらの加速試験技術は、高サイクル疲労（HCF）データの統計的なばらつきを効率的に扱うために不可欠なツールであり、設計に求められる信頼性レベル（例：\( -3\sigma \)の最小値）を確立するための基礎となります。

 

参考文献
/ High Cycle Fatigue A Mechanics of Materials Perspective T. Nicholas ELESEVIER 2006年
/ 超高サイクル疲労　Wikipedis 　2025/10/30閲覧
/ Review and Prospects for Current Studies on Very High Cycle Fatigue of Metallic Materials for Machine Structural Use Tatsui Sakai Journal od Solis Mechanics and Materials Engineering Vol.3 No.3 2009年

図表
図　Haigh線図　　出典： Fundamentals of Metal Fatigue Analysis J. A. Bannantine et al. Prentice Hall
図　二重S-N曲線の例；SUJ2　　出典： https://commons.wikimedia.org/w/index.php?
図　アルミニウム合金の超高サイクル疲労S-N曲線　出典：https://commons.wikimedia.org/w/index.php?
図　寿命分布を考慮したS-N曲線　　出典：High Cycle Fatigue　　Theodore Nicholas ELSEVIER 2006年
図　階段法により結果　　出典：High Cycle Fatigue　　Theodore Nicholas ELSEVIER 2006年
図　ステップテスト法の手順　　出典：High Cycle Fatigue　　Theodore Nicholas ELSEVIER 2006年

ORG:2025/11/03