1.2. 平均応力効果の定量化

1.2. 平均応力効果の定量化
（Quantifying mean stress effects）

アフィリエイト広告を利用しています。

Contents

1.2.1. 定寿命線図（ハイグ図）の基礎とHCF設計における必要性
1.2.2. ハイグ図を構成する応力パラメータとR一定線の幾何学的表現
1.2.3. 定寿命線の線形近似モデル：修正グッドマン線（Modified Goodman Equation）の適用
1.2.4. 非線形適合モデル：ガーバー、ジャスパー、SWTモデルの特性と平均応力の影響
1.2.5. 高応力比領域（\( R>0.7 \)）におけるハイグ図作成の課題と限界
1.2.6. 定寿命線図を決定するための効率的な試験技術と統計的評価
- - 1. ステップテスト法（Step Test Procedure）：
  - 2. 階段法（Staircase Method）：

1.2.1. 定寿命線図（ハイグ図）の基礎
とHCF設計における必要性

疲労サイクルを特徴づける応力変数として、最大応力（\( \sigma_{ max } \)）、最小応力（\( \sigma_{ min } \)）、平均応力（\( \sigma_{ m } \)）、交番応力（\( \sigma_{ alt } \)）、および応力比（\( R \)）の5つがありますが、これらのうち独立なパラメータは2つです。高サイクル疲労（HCF：High Cycle Fatigue）設計において、平均応力（\( \sigma_{ m } \)）は材料の疲労限度に非常に大きな影響を与えるため、その影響を定量的に扱うことが不可欠となります。
特に、ガスタービンエンジンや回転機械などの分野では、遠心力によって生じる平均応力は比較的明確に定まる一方で、振動などに起因する交番応力には大きな不確実性が伴います。したがって、これら二つの応力成分を設計基準として整理し、特定の寿命（通常、長寿命域である\( 10^7 \)サイクル以上）で破壊に至る境界を定義することが、安全かつ経済的な設計の基礎となります。
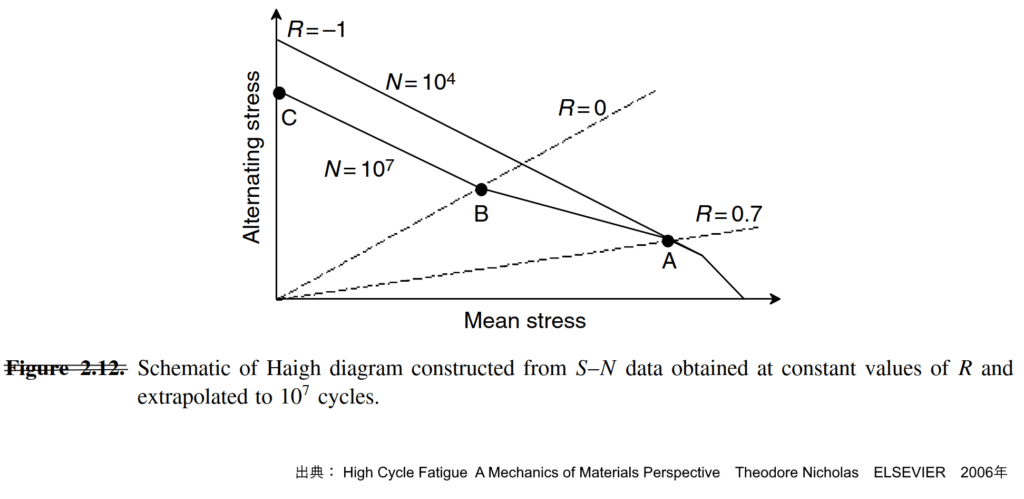
この目的のために用いられるのが定寿命線図（CLD：Constant Life Diagram）であり、その代表格がハイグ図（Haigh Diagram）です。ハイグ図は、横軸に平均応力\( \sigma_{ m } \)、縦軸に交番応力\( \sigma_{ alt } \)をとり、設定された一定の寿命（例えば\( 10^7 \)サイクル）で破壊に至る応力状態の軌跡を示す図です。ハイグ図は、特定のサイクル数に対応する疲労限度応力（FLS：Fatigue Limit Stress）を特徴づけるツールとして機能します。この図の一般的な形状は、正の平均応力が増加するにつれて、許容される交番応力レベルが低下する傾向を示しており、平均応力が疲労強度を低下させる影響を視覚的に示します。歴史的には、応力範囲（R：Range）と平均応力（M：Mean）のプロット、すなわちR-M線図やR/M線図とも呼ばれていました。

図　ハイグ図　出典： High Cycle Fatigue A Mechanics of Materials Perspective

1.2.2. ハイグ図を構成する
応力パラメータとR一定線の幾何学的表現

ハイグ図の縦軸には交番応力\( \sigma_{ alt } \)（応力範囲の半分）が、横軸には平均応力\( \sigma_{ m } \)が取られます。S-N曲線から特定の長寿命（例：\( 10^7 \)サイクル）に対応する疲労限度応力（FLS）を、異なる応力比\( R \)のデータから求め、そのFLSに対応する\( \sigma_{ m } \)と\( \sigma_{ alt } \)を計算してプロットすることで、ハイグ図上の点が決定されます。
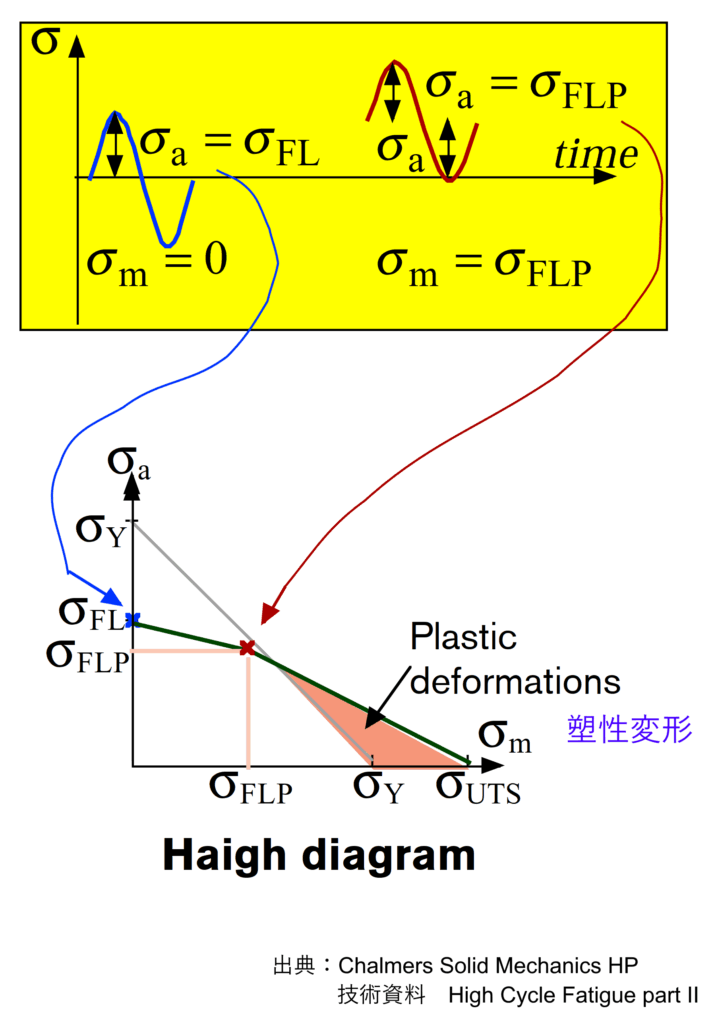
ハイグ図上において、応力比\( R \)が一定のデータ点は、原点（\( \sigma_{ m }=0, \sigma_{ alt }=0 \)）から放射状に伸びる直線として表現されます。これは、応力比\( R \)が\( R = (\sigma_{ m } – \sigma_{ alt }) / (\sigma_{ m } + \sigma_{ alt } )\)によって定義されるためです。例えば、完全両振り（\( R= -1 \)）のデータは、平均応力ゼロの縦軸（\( \sigma_{ alt } \)軸）上に位置します。一方、片振り引張（\( R = 0 \)）のデータは、\( \sigma_{ alt } = \sigma_{ m } \)の直線上に位置し、原点から45度に伸びる線となります。図の境界は、最大応力\( \sigma_{ max } = \sigma_{ m } + \sigma_{ alt } \)が材料の引張強度や降伏強度などの静的強度を超えない領域に制限されます。
ハイグ図は、特に回転機械の設計者にとって非常に有用です。なぜなら、設計者は計算や測定によって平均応力\( \sigma_{ m } \)を比較的正確に把握できる一方、振動から生じる交番応力\( \sigma_{ alt } \)には大きな不確実性が伴うため、この図を用いることで、許容される振動応力レベルを平均応力の関数として直接的に読み取ることができるためです。設計においては、平均応力がゼロである完全両振り（\( R= – 1 \)）のデータが多く使用されますが、実際の運用では\( R \)が高くなる傾向があるため、ハイグ図全体にわたる特性評価が重要です。

図　ハイグ図と強度の静的限界　出典：ファンクションベイ（株）様HP技術資料　第3章高サイクル疲労

1.2.3. 定寿命線の線形近似モデル：
修正グッドマン線（Modified Goodman Equation）の適用

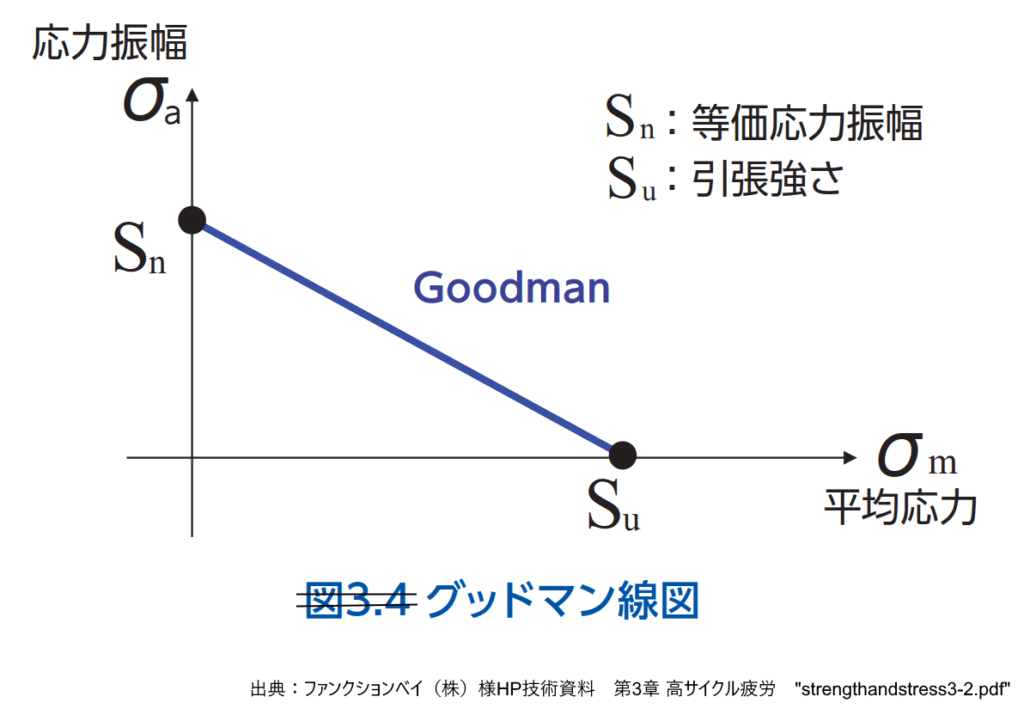
ハイグ図上の定寿命線（FLSの軌跡）を記述するための最も歴史があり、最も一般的に使われる経験的なモデルの一つが、修正グッドマン方程式（Modified Goodman Equation）です。このモデルは、ハイグ図上で、平均応力ゼロにおける疲労限度応力（\( S_{ 0 } \)または\( \sigma_{ alt, R=-1 } \)）と、交番応力ゼロにおける材料の最終引張強度（\( \sigma_{ ult } \)または\( S_{ u } \)）とを直線で結んだものとして描かれます。
修正グッドマン法則は、その直線近似の性質から、実際の実験データが示す非線形の形状（特に引張平均応力側で下に凸となる傾向）に比べて、より安全側の設計基準を提供します。この「安全側」という特性が、このモデルが設計基準として広く採用されている主要な理由です。グッドマンは、振動荷重が静的極限強度を決定する際に、平均荷重に加えて、交番荷重の2倍の合計が静的極限強度を超えてはならないという「動的理論」に基づいてこの直線を提案しました。このモデルは、数学的にシンプルで、容易に適用でき、覚えやすいという利点がありました。

図　グッドマン線図　出典： High Cycle Fatigue A Mechanics of Materials Perspective　Theodore Nicholas　ELSEVIER　2006年

ハイグ図はしばしばグッドマン線図と誤って呼ばれます。これは修正グッドマン線というモデルがあまりにも一般化した結果です。修正グッドマンの式は、応力振幅\( S_{ a } \)を\( S_{ a } = S_{ 0 } (1 – S_{ m } / S_{ u } )\)として表され、引張平均応力の影響を線形に考慮します。ただし、この線形モデルは、高平均応力（高\( R \)値）の領域での材料挙動を正確に捉えきれない可能性があり、特にこの領域でのデータ不足が課題となることがあります。

1.2.4. 非線形適合モデル：
ガーバー、ジャスパー、SWTモデルの特性と平均応力の影響

ハイグ図の実際の形状は非線形であることが多く、特に高い平均応力領域では線形近似のグッドマン線は不正確になる可能性があります。そのため、実験データにより適合する非線形モデルがいくつか提案されています。

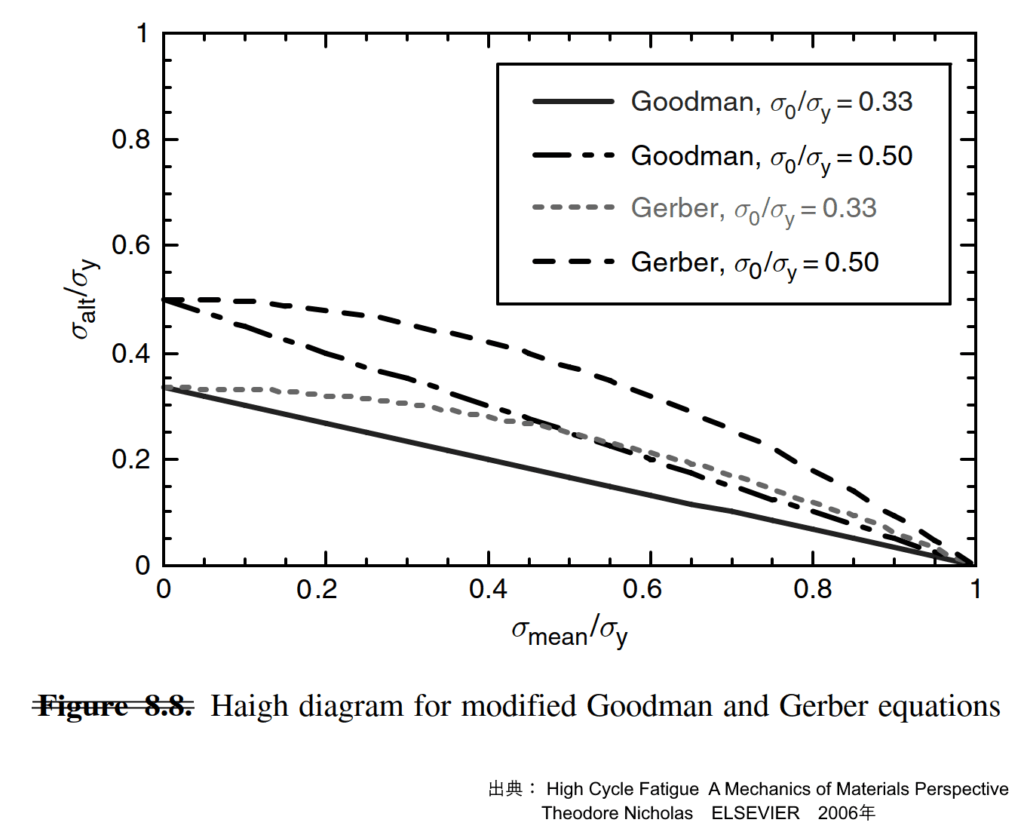
1. ガーバー放物線（Gerber parabola）：

これは疲労強度を最終引張強度の二乗で関連づけるモデルであり、ハイグ図上で放物線として描かれます。ガーバー放物線は、多くの場合、実験データにより適合する傾向を示しますが、グッドマン線よりも非安全側な予測となる場合があります。

図　ハイグ図におけるグッドマン線とガーバー放物線との比較　出典： High Cycle Fatigue A Mechanics of Materials Perspective

2. スミス・ワトソン・トッパー（SWT：Smith, Watson, Topper）の式：

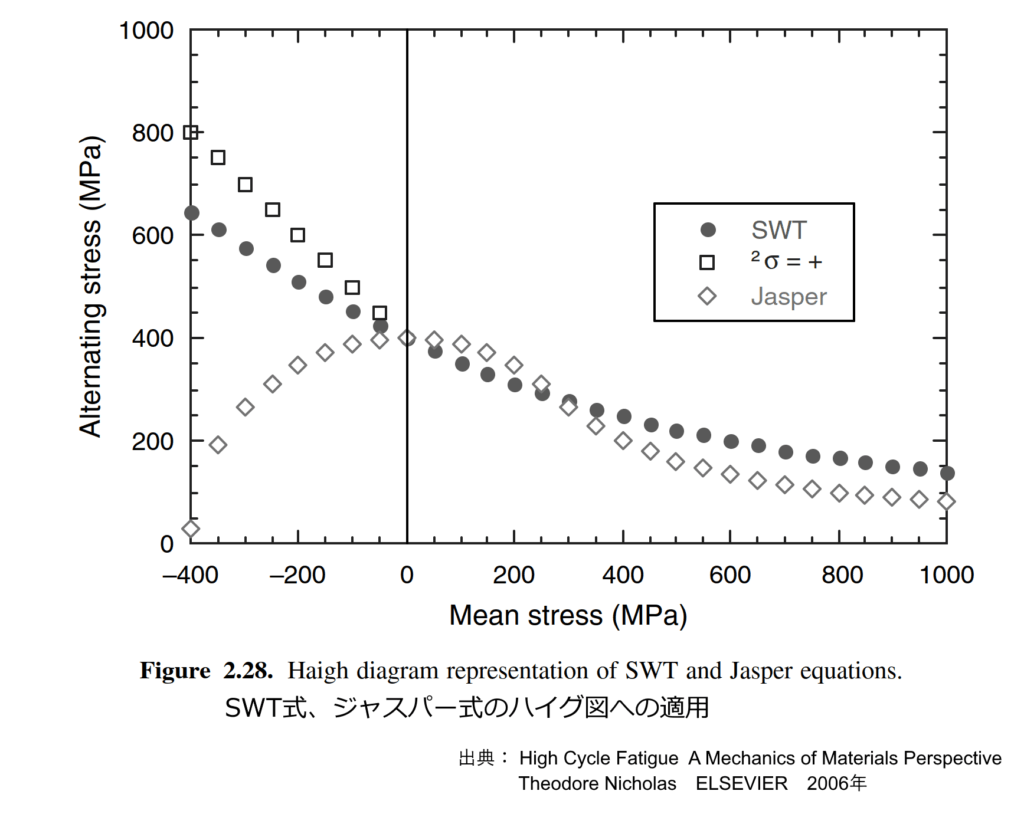
これは、応力比\( R \)が異なるデータを単一の曲線に統合しようとする試みの一つです。高サイクル疲労（HCF）の弾性領域では、SWT有効応力（\( \sigma_{ eff } = (\sigma_{ max } \sigma_{ a })^{ 1/2 } \)）として表現され、この有効応力が一定であるという条件でハイグ図の形状を定義できます。SWT式は、負の平均応力領域（圧縮側）において、平均応力がさらに負になるにつれて許容される交番応力が増加するという、上に凸の曲線を示す特徴的な形状をとります。SWT法による平均応力補正は、高サイクル領域で良好な結果を示すことが確認されていますが、平均応力が圧縮の場合は非安全側の評価になるため、引張応力の場合に限定して適用することが推奨されます。

3. ジャスパーの式（Jasper Equation）：

特定の材料（Ti-6Al-4Vなど）の実験データによく適合することが見出されているモデルであり、ハイグ図上でゼロ平均応力に対して対称的な形状を示す可能性があります。このモデルは、負の平均応力領域のデータを含めて、広範囲の応力比を表現するために使用されることがあります。

図　SWT式、ジャスパー式のハイグ図への適用　出典： High Cycle Fatigue A Mechanics of Materials Perspective

これらの非線形モデル、特にスミス・ワトソン・トッパー（SWT）の式やジャスパーの式は、平均応力効果をより正確に反映し、設計限界を定める上でより現実に近い評価を可能にします。

1.2.5. 高応力比領域（\( R>0.7 \)）におけるハイグ図作成の課題と限界

ハイグ図は、主に\( R= -1 \)（完全両振り）などの低平均応力条件で得られたS-N曲線データから構築されることが多いですが、実際の高サイクル疲労（HCF）設計では、高い平均応力（例：\( R=0.7 \)や\( R=0.9 \)）が支配的な領域でのデータが必要とされます。この高応力比領域は、高い平均応力に小さな振動応力が重畳される状態を表します。
しかし、この高\( R \)値領域では、利用可能なデータが非常に少ないため、低\( R \)値からの外挿による定寿命線図の構築は、その妥当性が疑わしい場合があります。また、低\( R \)値と高\( R \)値では疲労破壊の統計的分布が同じであるという仮定も疑問視されています。設計の観点からは、高\( R \)値（\( R>0.5 \)）では、交番応力\( \sigma_{ alt } \)よりも最大応力\( \sigma_{ max } \)がより重要な制限要因となるため、安全余裕を設定する際には両方のパラメータを考慮することが推奨されています。
さらに、ハイグ図の基本的な限界として、その作成が純粋な高サイクル疲労（HCF）荷重（き裂がない状態でのき裂発生寿命が支配的）に基づいている点が挙げられます。実機部品では、低サイクル疲労（LCF）や異物損傷（FOD：foreign object damage）などによって初期き裂や損傷が事前に導入されていることがあり、このような初期損傷が存在する場合、ハイグ図は材料の挙動を正確に表さなくなります。複合的な損傷（LCF-HCF相互作用など）を評価する場合、ハイグ図ではなく、破壊力学に基づいた損傷許容設計（Damage Tolerance）の概念が必要となります。このため、ハイグ図は「き裂発生寿命」を前提としていますが、実際の設計では初期欠陥の影響を排除できないことが課題となっています。

1.2.6. 定寿命線図を決定するための効率的な試験技術と統計的評価

ハイグ図を作成するために必要な、長寿命域における疲労限度応力（FLS：fatigue limit stress）のデータ点（\( \sigma_{ m } \)と\( \sigma_{ alt } \)の組）を効率的に得るためには、加速試験技術が不可欠です。疲労限度応力（FLS）の決定には、多くの試験片を長サイクル（\( 10^7 \)サイクル以上）まで試験する必要があるため、時間とコストの制約が大きいからです。
主要な加速試験手法には、以下の二つがあります。

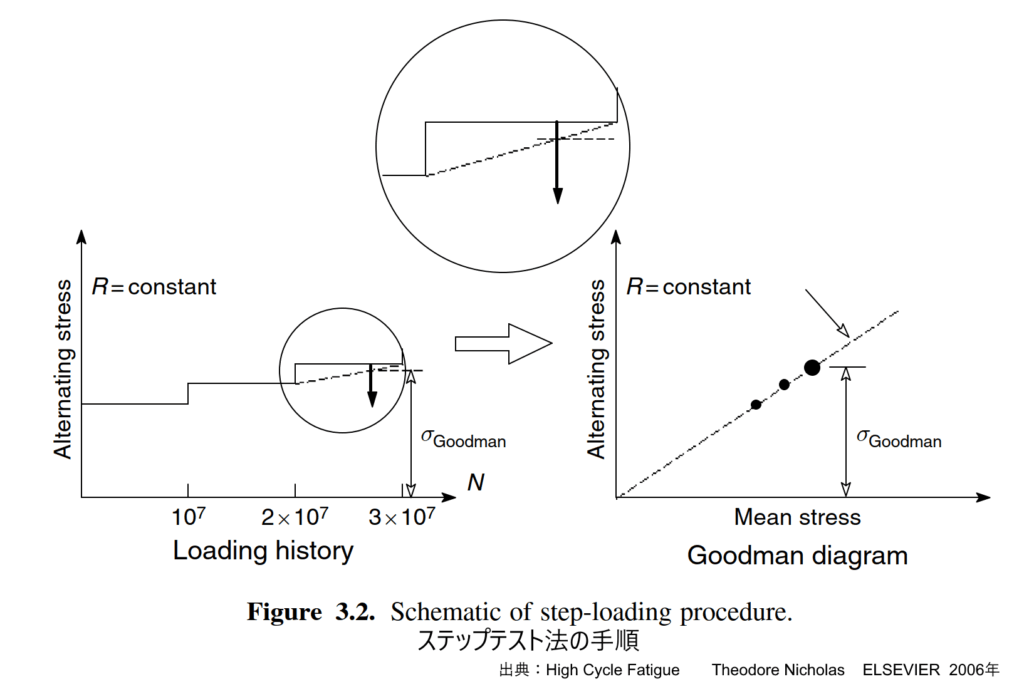
1. ステップテスト法（Step Test Procedure）：

この手法は、単一の試験片に対して応力レベルを段階的に増加（または減少）させていき、最終的な破壊応力または生き残り応力から疲労限度応力（FLS）を推定するものです。この方法の最大の利点は、各試験片から疲労限度応力（FLS）のデータ点が得られるため、限られたサンプル数でハイグ図を迅速に作成するのに特に有用であることです。ステップテスト法が、従来の定応力S-N試験から補間して得られた疲労限度応力（FLS）と一致することが、特に高\( R \)値領域で検証されています。

図　ステップテスト法の手順　出典： High Cycle Fatigue A Mechanics of Materials Perspective

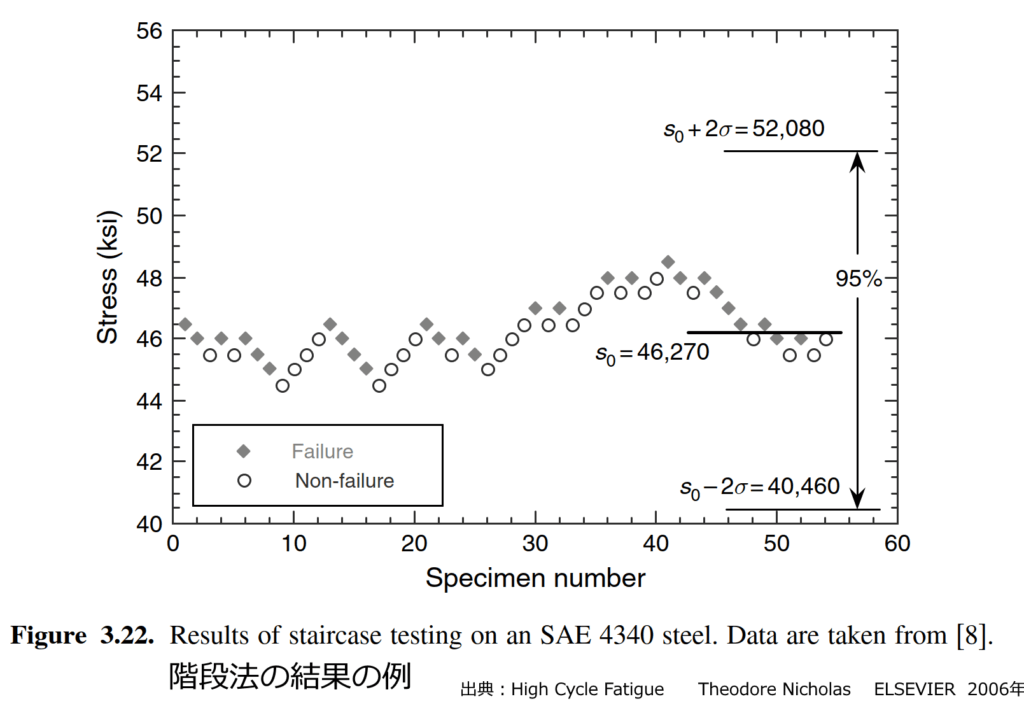
2. 階段法（Staircase Method）：

アップ・アンド・ダウン法とも呼ばれ、前の試験片が破壊したか（Failure）生き残ったか（Survival/Run-out）に応じて、次の試験の応力レベルを一定のステップサイズで上下させる統計的手法です。この方法は、特定のサイクル数における疲労限度応力（FLS）の中央値（Mean value）と標準偏差（Standard Deviation）を効率的に推定するために使用され、平均値の推定精度が高いという特徴があります。

図　階段法により結果　出典： High Cycle Fatigue A Mechanics of Materials Perspective

これらの加速試験技術により得られた平均応力と交番応力のデータ点は、ハイグ図上にプロットされ、グッドマン線やガーバー放物線などのモデルを用いて曲線適合（カーブフィッティング）されることで、設計基準となる定寿命線が決定されます。例えば、超高サイクル疲労（VHCF）領域における平均応力の影響を調査するために、階段法を用いて\( R= -1, 0, 0.5, 0.8 \)などの異なる応力比での疲労強度を決定し、それをハイグ図にまとめた研究例があります。

参考文献
/ High Cycle Fatigue A Mechanics of Materials Perspective T. Nicholas ELESEVIER 2006年
/ 超高サイクル疲労　Wikipedis 　2025/10/30閲覧
/ ファンクションベイ（株）様HP技術資料　第3章高サイクル疲労　”strengthandstress3-2.pdf”
/ Chalmers Solid Mechanics HP　技術資料　High Cycle Fatigue part II

図表
図　ハイグ図　　出典： High Cycle Fatigue A Mechanics of Materials Perspective
図　グッドマン線図　出典： High Cycle Fatigue A Mechanics of Materials Perspective　Theodore Nicholas　ELSEVIER　2006年
図　ハイグ図におけるグッドマン線とガーバー放物線との比較　出典： High Cycle Fatigue A Mechanics of Materials Perspective
図　SWT式、ジャスパー式のハイグ図への適用　出典： High Cycle Fatigue A Mechanics of Materials Perspective
図　階段法により結果　出典： High Cycle Fatigue A Mechanics of Materials Perspective
図　ステップテスト法の手順　出典： High Cycle Fatigue A Mechanics of Materials Perspective

ORG:2025/11/09