2.3.2 圧縮性流体の管路損失

2.3.2 圧縮性流体の管路損失
（Compressible fluid pipeline loss）

アフィリエイト広告を利用しています。

Contents

1. 圧縮性流体の基本特性と非圧縮性流体との違い
2. 圧縮性流体の管路損失を支配する基礎理論と力学的エネルギーバランス
- 2.1 圧縮性流体の管路損失
- 2.2 ポンプ配管系との対比
3. 実務で利用される主要な流動モデル（等温流とファノ線）の詳細解析
4. チョーク現象（音速流）の回避と安全設計上の考慮事項
5. 圧縮性流体設計のまとめ

1. 圧縮性流体の基本特性と非圧縮性流体との違い

配管技術者が直面する流体輸送の使命は、「要求される流量を確実かつ安全に目標の場所まで輸送すること」にあります。圧縮性流体、すなわち気体や蒸気（ガス）の管路設計においては、非圧縮性流体である液体とは根本的に異なる物理現象を扱う必要があります。この違いの核心は、流体の密度 \( \rho \) が、圧力 \( P \) や温度 \( T \) の変化によって大きく変動するという圧縮性流体の特性に起因します。

液体の場合は、流体の体積流量 \( Q \) が流路のどこにおいてもほぼ一定であるという連続の式に基づいて解析されます。液体は圧力が変化しても密度の変化が極めて小さいため、流速 \( V \) も一定と見なせ、管路損失（損失水頭 \( h_{ L } \) は主に直管摩擦と、バルブや継手などの抵抗（損失係数 \( \Sigma K \) によって計算されます。損失水頭 \( h_{ L } \) は、流量 \( Q \) のほぼ2乗に比例して求められます。

一方、圧縮性流体の場合、連続の式は質量流量 \( \dot{ m } \) が一定であるという形で適用されます（ \( \dot{ m } = \rho A w \)、ここで \( A \) は断面積、\( w \) は流速）。流体が管路を流れる際、摩擦（粘性抵抗）によって圧力が低下すると、ボイル・シャルルの法則に従い、流体の体積（比容積 \( v = 1 / \rho \)）が膨張します。その結果、質量流量を維持するために流速 \( w \) は必ず増加します。この流速の増加は、以下の二つの連鎖的な影響を及ぼします。

1. 運動エネルギー損失の増大：
流速が増加することにより、流体の持つ運動エネルギー（速度水頭）が増加します。この運動エネルギーの増加は、圧力水頭を取り崩してまかなわれるため、見かけ上、圧力損失を増大させる要因となります。

2. 摩擦損失の増大：
摩擦損失は流速の2乗にほぼ比例するため、流速の増加はさらなる摩擦損失を引き起こします。

このように、圧縮性流体の管路損失は、摩擦、運動エネルギーの変化、密度の変化が相互に絡み合いながら進行する複雑なプロセスです。したがって、非圧縮性流体に適用されるダーシー・ワイスバッハの式をそのまま適用することは原理的に誤りであり、配管設計者はこの流体の状態変化を厳密に扱うために、基礎理論（熱力学と流体力学）を熟知している必要があります。

2. 圧縮性流体の管路損失を支配する基礎理論と力学的エネルギーバランス

2.1 圧縮性流体の管路損失

圧縮性流体の管路損失を解析する際の基礎となるのは、力学的エネルギーバランス（Mechanical Energy Balance, MEB）です。これは、流動の過程で、流体の持つエンタルピー（内部エネルギーと流動エネルギーの和）、運動エネルギー、位置エネルギーが、外部からの仕事（ポンプなど）と、不可逆的な摩擦損失（熱として消費される損失）によってどのようにバランスしているかを示すものです。

単位質量あたりの微分形式（オイラーの式を熱力学的に拡張したもの）で考えると、管路内の微小区間における圧力損失 \( dP \) は以下の項目の合算として表現されます。

\( -\displaystyle\frac{ dP }{ \rho } = d \left( \displaystyle\frac{ w^2 }{ 2 }\right) + g dz + d(\text{不可逆損失}) \)

本式で、各項が示す物理的意味は以下の通りです。
1. 摩擦損失項（ \( d( \text{不可逆損失}) \)）：
これは、流体と管壁との粘性摩擦、および流体内部の粘性抵抗によって発生する不可逆的なエネルギー損失です。これは、非圧縮性流体の場合と同様に、ファンニングの式に基づき、管長 \( L \)、摩擦係数 \( f \)、流速 \( w \)、管内径 \( D \) を用いて表されます。圧縮性流体の場合、流速 \( w \) は流下に伴い連続的に変化するため、この項は区間ごとに流速変化を考慮して積分する必要があります。

2. 運動エネルギー変化項（\( d(w^2/2) \)）：
前述の通り、圧力が低下すると密度 \( \rho \) が減少し、連続の式を保つために流速 \( w \) が加速します。この項は、加速に伴う運動エネルギーの増加分（動圧損失）を示します。液体ではこの項は通常無視できるか、レジューサ部などで速度水頭が増減する程度ですが、気体では流路全体で支配的な役割を果たします。

3. 位置エネルギー変化項（ \( g dz \)）：
これは、配管の標高差 \( dz \) に伴う位置エネルギーの変化です。ガスの場合は密度が非常に小さいため、この静水頭の変化による圧力への影響は極めて小さく、水平配管の計算においては通常無視されます。ただし、液体を扱うポンプシステムの実揚程 \( H \) を計算する際には、位置水頭の差 \( Z_{ 2 } – Z_{ 1 } \) は重要な要素となります。

2.2 ポンプ配管系との対比

液体を扱うポンプ系の設計では、ポンプ全揚程 \( H \) は、実揚程（位置水頭の差）と、配管系全体の摩擦損失水頭 \( h_{ L } \) の和として決定されます。ポンプと配管系の運転点は、ポンプの全揚程曲線と、配管系のシステム抵抗曲線 \( h_{ L } = \alpha Q^2 \) の交点として定まります。圧縮性流体の解析は、この「水頭」の概念ではなく、「圧力」と「エンタルピー」の概念で熱力学的な状態変化を追跡するという点で、より高度な物理的理解が求められます。

3. 実務で利用される主要な流動モデル（等温流とファノ線）の詳細解析

圧縮性流体の管路解析を行う際、流動中に発生する熱的な挙動（周囲との熱交換の有無）をどのように仮定するかにより、主要なモデルが使い分けられます。

3.1 等温流モデル（Isothermal Flow Model）

このモデルは、流体が非常に長い配管を流れる場合、または配管が周囲環境と活発に熱交換を行い、流体温度 \( T \) が全区間にわたって一定に保たれると仮定する場合に適用されます。
・適用例：長距離の天然ガス輸送パイプラインなど。パイプラインが地中に埋設されている場合、地温によって流体温度が一定に保たれやすいです。
・特徴：温度 \( T \) が一定であるため、理想気体を仮定すれば、圧力 \( P \) と比容積 \( v \) の積 \( Pv \) は一定となります（ \( Pv = RT = \text{const.} \)）。このモデルで導出される圧力損失の計算式は、主に摩擦損失と流速変化による運動エネルギー損失の項を含み、実務で広く利用されています。長距離輸送では、摩擦損失が支配的であり、運動エネルギー変化は相対的に小さくなる傾向があります。

3.2 断熱流（ファノ線）モデル（Fanno Line Model）

このモデルは、周囲との熱交換がない（断熱）条件で、一定断面積の管路内を流れる流体の状態変化を記述します。
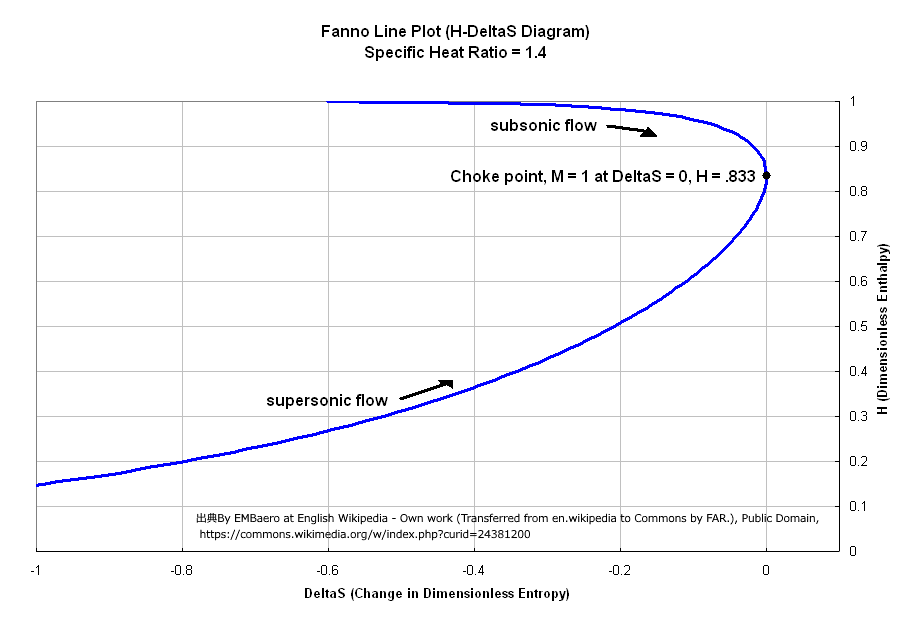
・基礎理論（熱力学）：ファノ線は、流体のよどみエンタルピー \( h_{ 0 } \) が一定であるという制約の下、摩擦損失によるエントロピー \( s \) の増加を許容しながら、流体の状態（圧力 \( P \)、温度 \( T \)、流速 \( w \)）がどのように変化するかを示す軌跡です。ファノ線上の流れは、常にエントロピーが増加する方向（流れ方向）に移動します。
・適用例：断熱材で覆われた短いダクト、ノズルやオリフィスなどの絞り後の高速の流れ、および熱交換の影響が無視できる短距離の高速配管。
・特徴：流れが速くなるにつれて（マッハ数 \( Ma \) が増加）、流体のエントロピーは増大します。このエントロピー増加の最大点が \( Ma=1 \)、すなわち音速点（チョーク点）に対応します。ファノ線は、摩擦が存在する限り、下流側で音速に達し得ることを示しており、音速を超えた超音速流は、定常的な摩擦流動では実現できません。ただし、ファノ線が記述するのは、摩擦のみが寄与する状態変化であり、熱交換がある場合はレイリー線（Rayleigh Line）など、別のモデルを適用します。

図　Fenno Line Plot　　出典：Wikipedia

3.3 実在気体の取り扱い（圧縮係数 \( Z \)）

高圧プロセスにおいては、理想気体の状態方程式（ \( PV = nRT \) ）からのズレが無視できません。特に、高圧・高温、または極低温のガスを取り扱う場合、実在気体の状態を記述するために圧縮係数 \( Z \) が導入されます（ \( PV = ZRT \) ）。
・エンタルピー計算への応用：理想気体ではエンタルピー \( H \) は温度のみの関数ですが、実在気体では圧力にも依存します。実在気体のエンタルピー \( H \) は、仮想的な理想気体のエンタルピー \( H^* \) に、圧力や温度による補正項を加えることで求められます。この補正項の計算には、圧縮係数 \( Z \) の情報や、臨界温度 \( T_{ c } \) および臨界圧力 \( P_{ c } \) を用いた対臨界値を用いた線図（Z線図）が利用されます。
・設計上の重要性：\( Z \) が1から大きく外れる条件では、密度の計算や、流速変化に伴う運動エネルギーの変化の評価が狂い、配管のサイズ選定や安全弁の容量計算に重大な誤差が生じるため、実在気体の補正は必須の技術となります。

4. チョーク現象（音速流）の回避と安全設計上の考慮事項

圧縮性流体の管路設計における最大の安全課題の一つは、チョーク現象（Choking, 音速流の発生）です。流体が音速に達すると、下流側の圧力をいくら低下させても、それ以上流量が増加しなくなります。

4.1 チョーク現象のメカニズムと影響

ファノ線モデルが示すように、摩擦や急激な断面積変化（バルブの絞りなど）によって流体のマッハ数 \( Ma \) が1に達する箇所が発生した場合、流れが閉塞（チョーク）します。チョーク流が発生すると、以下の問題が引き起こされます。

1. 流量制限：必要な流量が確保できず、プロセス能力が制約されます。
2. 圧力波伝播の制限：上流側からの圧力変動や流量調整信号が、チョーク点（音速点）を越えて下流側に伝わらなくなります。
3. 高周波振動・騒音：チョーク付近では流体の速度勾配や乱れが激しくなり、配管の壁面に作用する変動力が大きくなります。特に絞り弁や減圧オリフィスなどの絞り後の高速流体は、小口径配管や剛性の低い配管において高周波の振動を引き起こしやすく、設備の健全性を脅かします。

4.2 チョーク流の回避策

配管設計では、流速が音速に達しないように管径を十分に大きく設計することが基本です。特に流体の膨張や絞りが予想される箇所（安全弁出口、減圧弁下流など）では、流速を音速の0.5〜0.7倍程度に抑えることが推奨されます。

また、流体関連振動（Flow Induced Vibration）の対策として、流体の運動量の変化や圧力脈動がエルボや分岐などの壁に働く変動力となり、起振力となることを理解しておく必要があります。振動を避けるためには、流速を抑えることに加え、以下の対策が重要です。

・配管支持設計の最適化：回転機器（ポンプ、圧縮機など）の振動数が配管の固有振動数と一致する機械振動の共振を避けるよう、サポート間隔を調整します。配管サポートは、垂直荷重を支持するハンガ（リジット、スプリング、コンスタントなど）や、動きを拘束・制限するレストレイント、スナッバ（地震やサージングなどの急速な動きを拘束）を適切に配置する必要があります。
・流体励起振動の抑制：絞りやエルボ付近で発生する激しい乱れやカルマン渦による振動を抑制するため、可能な限り直線長さを確保し、急激な流路変更を避けます。

4.3 爆発波と安全距離の確保

高圧ガスプラントにおいては、配管内を流れるガスが何らかの異常で爆発性混合物となり、爆ごう波（衝撃波と燃焼波が一体となって超音速で進む化学反応）が発生するリスクを想定する必要があります。

爆ごう波やそれに伴う爆風効果は、ガラス破壊など甚大な被害をもたらします。高圧ガス保安法などでは、この爆風を基準に保安物件（民家や重要文化財など）に対する保安距離が定められています。設計技術者は、配管の強度設計に加え、万一の事故の際に、周辺の安全を確保するための距離や、爆発事故の誘因となる要因（配管からの漏えいによる蒸気雲爆発など）を排除するプロセス安全設計に責任を持つ必要があります。

5. 圧縮性流体設計のまとめ

圧縮性流体の管路設計は、非圧縮性流体の設計に比べ、熱力学的状態変化、実在気体効果、そして流速が音速に達する可能性という、多岐にわたる複雑な要因を総合的に評価することが求められます。
特に、圧力低下が流速増加を招き、それがまた圧力損失を増大させるという相互作用を正確に評価する能力が、プロセス安全の根幹となります。

参考文献
「配管設計」実用ノート　　西野悠司　日刊工業新聞社　2017年
PIPING HANDBOOK 7th ed 　Mohhinder L. Nayyar P.E. MacGraw-Hill　2000年
Fenno Flow　　Wikipedia 2025/10/08確認

図表
図　Fenno Line Plot　　出典：Wikipedia

ORG:2025/10/08